Jensens's inequality is a probabilistic inequality that concerns the expected value of convex and concave transformations of a random variable.
Jensen's inequality applies to convex and concave functions.
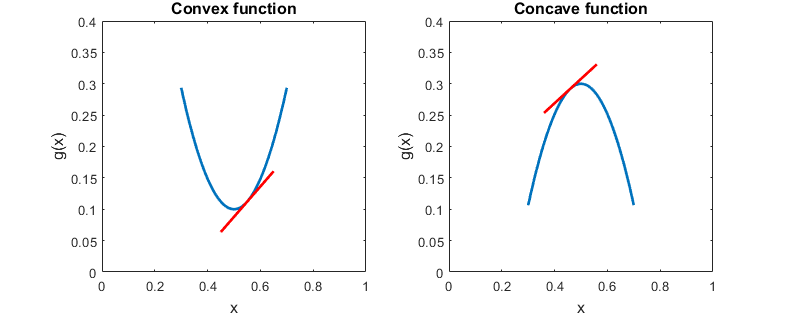
The properties of these functions that are relevant for understanding the proof of the inequality are:
the tangents of a convex function lie entirely below its graph;
the tangents of a concave function lie entirely above its graph.
Also remember that a differentiable function is:
(strictly) convex if its second derivative is (strictly) positive;
(strictly) concave if its second derivative is (strictly) negative.
The following is a formal statement of the inequality.
Proposition
Let
be an integrable random
variable. Let
be a convex function such
that
is
also integrable. Then, the following inequality, called Jensen's inequality,
holds:
A function
is convex if, for any point
the graph of
lies entirely above its tangent at the point
:
![]() where
where
is the slope of the tangent. Setting
and
,
the inequality
becomes
By
taking the expected value of both sides of the inequality and using the fact
that the expected value operator preserves
inequalities, we
obtain
![[eq7]](/images/Jensen-inequality__14.png)
If the function
is strictly convex and
is not almost surely constant, then
we have a strict
inequality:
A function
is strictly convex if, for any point
the graph of
lies entirely above its tangent at the point
(and strictly so for points different from
):
![]() where
where
is the slope of the tangent. Setting
and
,
the inequality
becomes
![]() and,
of course,
and,
of course,
when
.
Taking the expected value of both sides of the inequality and using the fact
that the expected value operator preserves inequalities, we
obtain
![[eq14]](/images/Jensen-inequality__30.png) where
the first inequality is strict because we have assumed that
where
the first inequality is strict because we have assumed that
is not almost surely constant and therefore the
event
does
not have probability
.
If the function
is concave,
then
If
is concave, then
is convex and by Jensen's
inequality:
Multiplying
both sides by
and
using the linearity of the expected value we obtain the result.
If the function
is strictly concave and
is not almost surely constant,
then
Similar to previous proof.
Suppose that a strictly positive random variable
has expected
value
and
it is not constant with probability one.
What can we say about the expected value of
,
by using Jensen's inequality?
The natural logarithm is a strictly concave function because its second
derivativeis
strictly negative on its domain of definition.
As a consequence, by Jensen's inequality, we
have![]()
Therefore,
has a strictly negative expected value.
Jensen's inequality has many applications in statistics. Two important ones are in the proofs of:
If you like this page, StatLect has other pages on probabilistic inequalities:
Below you can find some exercises with explained solutions.
Let
be a random variable having finite mean and variance
.
Use Jensen's inequality to find a bound on the expected value of
.
The function we need to study
isIt
has first
derivative
and
second
derivative
The
second derivative is strictly positive on the domain of definition of the
function. Therefore, the function is strictly convex. Furthermore,
is not almost surely constant because it has strictly positive variance.
Hence, by Jensen's
inequality:
![]() Thus,
the bound
is
Thus,
the bound
is
Let
be a positive integrable random variable.
Find a bound on the mean of
.
The function we need to study
isIt
has first
derivative
and
second
derivative
The
second derivative is negative on the domain of definition of the function.
Therefore, the function is concave and Jensen's inequality
gives:
![]() Thus,
the bound
is
Thus,
the bound
is
Please cite as:
Taboga, Marco (2021). "Jensen's inequality", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/Jensen-inequality.
Most of the learning materials found on this website are now available in a traditional textbook format.